Lecture Notes

7. Inverses and Isomorphisms

Part of the Series on Linear Algebra.

By Akshay Agrawal. Last updated Dec. 9, 2017.

Previous entry: ; Null Spaces and Ranges Next entry: Column Rank Equals Row Rank

In this section, we introduce the inverse of a linear map, and we use the notions of injectivity and surjectivity to characterize it. Intuitively, a linear map is invertible if there exists another linear map such that the composition of the two yields the identity map; the existence of an invertible map between two vector spaces tells us that the two spaces are in some sense equivalent, an idea that we’ll make precise shortly.

7.1 The Inverse of a Linear Map

Definition 7.1 A linear map $T: V \rightarrow W$ is invertible if there exists another linear map $S: W \rightarrow V$ such that $ST$ equals the identity map on $V$ (i.e., $ST(v) = v$ for all $v \in V$) and $TS$ equals the identity map on $W$ (i.e., $TS(w) = w$ for all $w \in W$). Such a map $S$ is called the inverse of $T$.

Note that in the above definition we say that $S$ is the inverse of $T$; implicit in our definition is the fact that an invertible linear map has a unique inverse. To see why this is true, let $S_1$ and $S_2$ be inverses of $T$. Then

$$S_1 = S_1I = S_1(TS_2) = (S_1T)S_2 = IS_2 = S_2,$$

i.e., $S_1 = S_2$. Uniqueness allows us to denote the inverse of $T$ with a single symbol; by convention, this symbol is $T^{-1}$.

Theorem 7.2.A map is invertible if and only if it is both injective and surjective.

Theorem 7.2 should be intuitive, because a map that is both injective and surjective looks something like this:

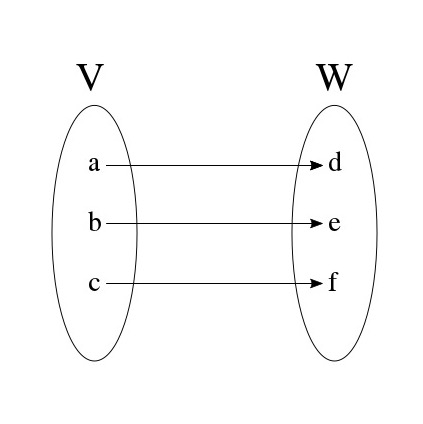
As the picture illustrates, an invertible linear map from $V$ to $W$ can be thought of as a reversible relabeling of all the points in V to all the points in W. You should take the time to prove theorem 7.2, even if you find it intuitive.

7.2 Isomorphisms

Definition 7.3 Two vector spaces $V$ and $W$ are said to be isomorphic if there exists an invertible linear map between them, and an invertible linear map, i.e., a map that is both injective and surjective, is said to be an isomorphism between $V$ and $W$.

When two vector spaces are isomorphic, we often say that they are “equivalent, up to relabeling.” The map illustrated in the previous section is an informal example of this: each letter in $V$ is relabeled to a unique letter in $W$, and likewise each letter in $W$ is relabeled to a unique letter in $V$.

For an analogy of what it means for two vector spaces to be isomorphic, imagine that $V$ and $W$ are two different natural languages such that both languages are capable of expressing exactly the same set of concepts and such that each language has exactly one word for every concept (i.e., words don’t have synonyms). Then every word in $V$ can be translated to a unique word in $W$ (injectivity), and every word in $W$ can be translated back to a unique word in $V$ (surjectivity). We might refer to this correspondence between concepts expressable in $V$ and concepts expressable in $W$ by saying that the two languages are equivalent, up to a relabeling of the concepts (the two languages use different words to refer to the same concept).

Theorem 7.4. Two vector spaces are isomorphic if and only if they have the same dimension.

The proof of theorem 7.4 is fairly straightforward; as a hint, you might find the Rank-Nullity theorem helpful in proving it.

7.3 Linear Operators

A linear map $T: V \rightarrow V$ from one vector space back to itself is called a linear operator.

Theorem 7.5 For a finite-dimensional vector space $V$ and a linear operator $T : V \rightarrow V$, the following are equivalent:

(a) T is invertible; (b) T is injective; (c) T is surjective.

Note that theorem 7.5 is not true for infinite-dimensional vector spaces.

7.4 Exercises

1. Prove theorem 7.2.
2. Prove theorem 7.4.
3. Prove theorem 7.5.

7.5 References

Linear Algebra Done Right, by Sheldon Axler.