$$ \newcommand{\qed}{\tag*{$\square$}} \newcommand{\span}{\operatorname{span}} \newcommand{\dim}{\operatorname{dim}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\norm}[1]{\|#1\|} \newcommand{\grad}{\nabla} \newcommand{\prox}[1]{\operatorname{prox}_{#1}} \newcommand{\inner}[2]{\langle{#1}, {#2}\rangle} \newcommand{\mat}[1]{\mathcal{M}[#1]} \newcommand{\null}[1]{\operatorname{null} \left(#1\right)} \newcommand{\range}[1]{\operatorname{range} \left(#1\right)} \newcommand{\rowvec}[1]{\begin{bmatrix} #1 \end{bmatrix}^T} \newcommand{\Reals}{\mathbf{R}} \newcommand{\RR}{\mathbf{R}} \newcommand{\Complex}{\mathbf{C}} \newcommand{\Field}{\mathbf{F}} \newcommand{\Pb}{\operatorname{Pr}} \newcommand{\E}[1]{\operatorname{E}[#1]} \newcommand{\Var}[1]{\operatorname{Var}[#1]} \newcommand{\argmin}[2]{\underset{#1}{\operatorname{argmin}} {#2}} \newcommand{\optmin}[3]{ \begin{align*} & \underset{#1}{\text{minimize}} & & #2 \\ & \text{subject to} & & #3 \end{align*} } \newcommand{\optmax}[3]{ \begin{align*} & \underset{#1}{\text{maximize}} & & #2 \\ & \text{subject to} & & #3 \end{align*} } \newcommand{\optfind}[2]{ \begin{align*} & {\text{find}} & & #1 \\ & \text{subject to} & & #2 \end{align*} } $$

6. Null Spaces and Ranges

Part of the Series on Linear Algebra.

By Akshay Agrawal. Last updated Dec. 9, 2017.

Previous entry: Interpretations of Linear Maps; Next entry: Inverses and Isomorphisms

Every linear map sends at least one vector in its domain to the zero vector. It is sometimes the case that a map sends non-zero vectors to the zero vector as well — an extreme example is the zero map. The set of vectors collapsed to zero and the complement of that are two key attributes of linear maps, as they in some loose sense capture the number of degrees of freedom that a map posseses. We formalize this idea in this section by studying null spaces and ranges.

6.1 Null Space and Range

Definition 6.1 The null space of a linear map $T$, denoted by $\null{T}$, is the set of vectors $v$ such that $Tv = 0$ for all $v \in \null{T}$. A synonym for null space is kernel.

Definition 6.2 The range of a linear map $T$, denoted by $\range{T}$, is the set of vectors $w$ such that $Tv = w$ for some $v \in W$. A synonym for range is image.

You should verify that both the null space and the range of linear map $T : V \rightarrow W$ are subspaces of $V$.

6.2 The Fundamental Theorem of Linear Maps (Rank-Nullity)

Intuitively, the dimension of the range of a linear map $T$ tells us how many degrees of freedom $T$ has, and the dimension of its null space tells us how degenerate it is. These are, apparently, two sides of the same coin, and this symmetry can be made precise via the following theorem.

Theorem 6.3: Rank-Nullity. Let $T : V \rightarrow W$ be a linear map. Then $\range T$ is finite-dimensional and

Proof sketch. Let $u_1, \ldots, u_m$ be a basis for $\null T$, and extend this list of vectors to a basis of $V$ of the form $u_1, \ldots, u_m, v_1, \ldots, v_n$. Show that $v_1, \ldots, v_n$ spans $\range T$, and also show that $Tv_1, \ldots, Tv_n$ is linearly independent. Conclude that $\dim V = \dim \range T + \dim \null T$.

6.3 Injectivity and Surjectivity

Definition 6.4 A linear map $T : V \rightarrow W$ is injective if $Tu = Tv$ implies $u=v$ for all vectors $u$ and $v$ in $V$.

Null space and injectivity are intimately tied: a linear map is injective if and only if its null space is $\{0\}$.

A synonym for “injective” is one-to-one. You can think of an injective map as one that injects a smaller space into a larger or equally sized one. Indeed, there exists an injective linear map from $V$ to $W$ if and only if $\dim V \leq \dim W$ (use the rank-nullity theorem to prove this to yourself).

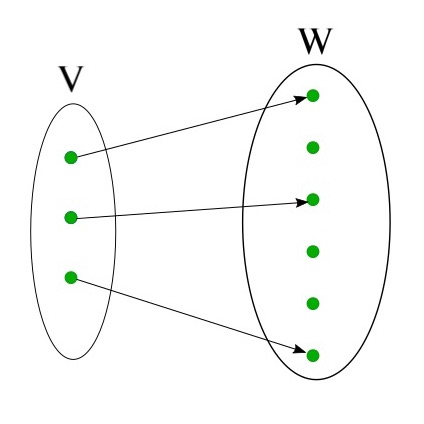
An injective map injects a smaller space into a larger one (or possibly into an equally sized one).

Definition 6.5 A linear map $T : V \rightarrow W$ is surjective if for every $w \in W$ there exists some $v \in V$ such that $Tv = w$, that is, if $\range T = W$.

A synonym for “surjective” is onto, in the sense that $T$ is surjective if its range completely covers $W$. It should be intuitive that there exists a surjective linear map from $V$ to $W$ if and only $\dim V \geq \dim W$ (again, use the rank-nullity theorem to prove this to yourself).

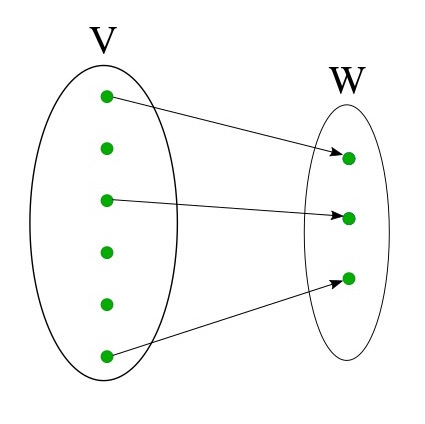
A surjective map $$T : V \to W$$ covers $$W$$ with elements from a vector space $$V$$ that is at least as large as $$W$$.

6.4 Exercises

1. Flesh out the proof sketch of the rank-nullity theorem.
2. Prove the claims about injectivity and surjectivity that are made in section 6.3.
3. Prove that any homogeneous system of linear equations with more variables than equations has nonzero solutions.
4. Prove that there exists a vector $b \neq 0$ such that an inhomogeneous system of linear equations $Ax = b$ with more equations than variables has no solution.
5. Prove that $\dim \range{ST} \leq \min \{ \dim \range S, \dim \range T \}$, where $S: V \rightarrow W$ and $T: U \rightarrow V$ are linear maps.
6. Prove that $\dim \null{ST} \leq \dim \null S + \dim \null T$, where $S: V \rightarrow W$ and $T: U \rightarrow V$ are linear maps.

6.5 References

Linear Algebra Done Right, by Sheldon Axler.