$$ \newcommand{\qed}{\tag*{$\square$}} \newcommand{\span}{\operatorname{span}} \newcommand{\dim}{\operatorname{dim}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\norm}[1]{\|#1\|} \newcommand{\grad}{\nabla} \newcommand{\prox}[1]{\operatorname{prox}_{#1}} \newcommand{\inner}[2]{\langle{#1}, {#2}\rangle} \newcommand{\mat}[1]{\mathcal{M}[#1]} \newcommand{\null}[1]{\operatorname{null} \left(#1\right)} \newcommand{\range}[1]{\operatorname{range} \left(#1\right)} \newcommand{\rowvec}[1]{\begin{bmatrix} #1 \end{bmatrix}^T} \newcommand{\Reals}{\mathbf{R}} \newcommand{\RR}{\mathbf{R}} \newcommand{\Complex}{\mathbf{C}} \newcommand{\Field}{\mathbf{F}} \newcommand{\Pb}{\operatorname{Pr}} \newcommand{\E}[1]{\operatorname{E}[#1]} \newcommand{\Var}[1]{\operatorname{Var}[#1]} \newcommand{\argmin}[2]{\underset{#1}{\operatorname{argmin}} {#2}} \newcommand{\optmin}[3]{ \begin{align*} & \underset{#1}{\text{minimize}} & & #2 \\ & \text{subject to} & & #3 \end{align*} } \newcommand{\optmax}[3]{ \begin{align*} & \underset{#1}{\text{maximize}} & & #2 \\ & \text{subject to} & & #3 \end{align*} } \newcommand{\optfind}[2]{ \begin{align*} & {\text{find}} & & #1 \\ & \text{subject to} & & #2 \end{align*} } $$

1. Vector Spaces

Part of the Series on Linear Algebra.

By Akshay Agrawal. Last updated July 30, 2017.

Next entry: Subspaces

The fundamental object of study in linear algebra is the vector space; linear algebra in its entirety is nothing more than the study of linear maps onto vector spaces. As we shall soon see, vector spaces are quite simple objects. It is satisfying that their study yields both an aesthetic theory and a practical toolbelt indispensable for almost anyone working in an engineering discipline.

In these notes, we define vector spaces and reify the definition with a series of simple examples.

1.1 Definition

Consider a set of objects that is closed under addition and scalar multiplication. If you can guarantee that such a set also (1) contains additive and multiplicative identities (think $0$ and $1$), additive inverses (think $-v$), and (2) obeys commutativity, associativity, and the distributive law, then that set is in fact a vector space. Here’s the full definition.

Definition 1.1 A vector space is a set $V$, paired with an addition and a scalar multiplication on a field $\Field$, satisfying the following six properties:

1. Commutativity: $u + v = v + u \; \forall u, v \in V$.
2. Associativity: $(u + v) + w = u + (v + w) \; \forall u, w, v \in V$ and $a(bv) = (ab)v$ $\; \forall a, b \in \mathbb{F}, v \in V$.
3. Additive Identity: There exists $0 \in V$ such that $u + 0 = u$, for all $u \in V$.
4. Additive Inverse: For every $u \in V$, there exists an element $w \in V$ such that $u + w = 0$.
5. Multiplicative Identity: There exists an element $1 \in \mathbb{F}$ such that $1u = u$ for all $u \in V$.
6. Distributive Law: $a(u + v) = av + aw$ for all $a \in \mathbb{F}$, $u, v \in V$. Similarly $(a + b)u = au + bu$.

For the purposes of these notes, you can think of the scalars as originating from either the real numbers $\Reals$ or the complex numbers $\Complex$: that is, feel free to take the field (see the aside) $\Field$ as either $\Reals$ or $\Complex$, unless we say otherwise.

Aside. Scalar multiplication on a set is defined over a field $\Field$, and a vector space is in turn defined over the field used by its scalar multiplication. A field is a set that is equipped with two commutative and associative operations, addition and multiplication; these operations also have identities ($0$ and $1$, respectively) and inverses (the identity $0$ is not required to posses a multiplicative inverse), and the two operations are linked by a distributive law. In most practical problems, the encountered vector spaces are over either $\Reals$ or $\Complex$.

1.2 Examples

You’ve certainly worked with vector spaces before, even if you haven’t called them as such. The real line $\Reals$ is a vector space, as is the two-dimensional plane $\Reals^2$. More generally, the $n$-dimensional space $\Reals^n$, where every vector or point has $n$ coordinates, is a vector space. The complex analogues of these spaces are also vector spaces. A good but admittedly tedious exercise is to verify for yourself that these objects are all in fact vector spaces.

While the objects in a vector space are called “vectors,” they need not be vectors in the sense you might have come across in physics (what’s in a name, anyway?). For example, the set of functions from a set $S$ to a field $\Field$, denoted $\Field^S$, is a vector space (if addition and scalar multiplication are defined in the natural way). In particular, the elements of $\Field^S$ are functions. We won’t use this example in the sequel, but it’s worthwhile to keep in mind that the definition of a vector space is an expressive one.

1.3 Why You Should Care

The first reason that you should care about vector spaces is cultural literacy: if you are at all (and I really mean at all) interested in speaking mathematics, then you simply must be fluent in linear algebra. And if you are at all interested in applying mathematics, then, well, the same applies.

As for applications: it is nonsensical to speak about the applications of vector spaces, as vector spaces are not things you apply. But you’ll be dealing with vector spaces whenever you’re applying linear algebra — as we noted earlier, linear algebra is but the study of linear maps onto vector spaces. If you’re reading these notes with an eye towards machine learning, you should know that most models encode their data as vectors that lie in some vector space (usually $\Reals^n$ for some $n$).

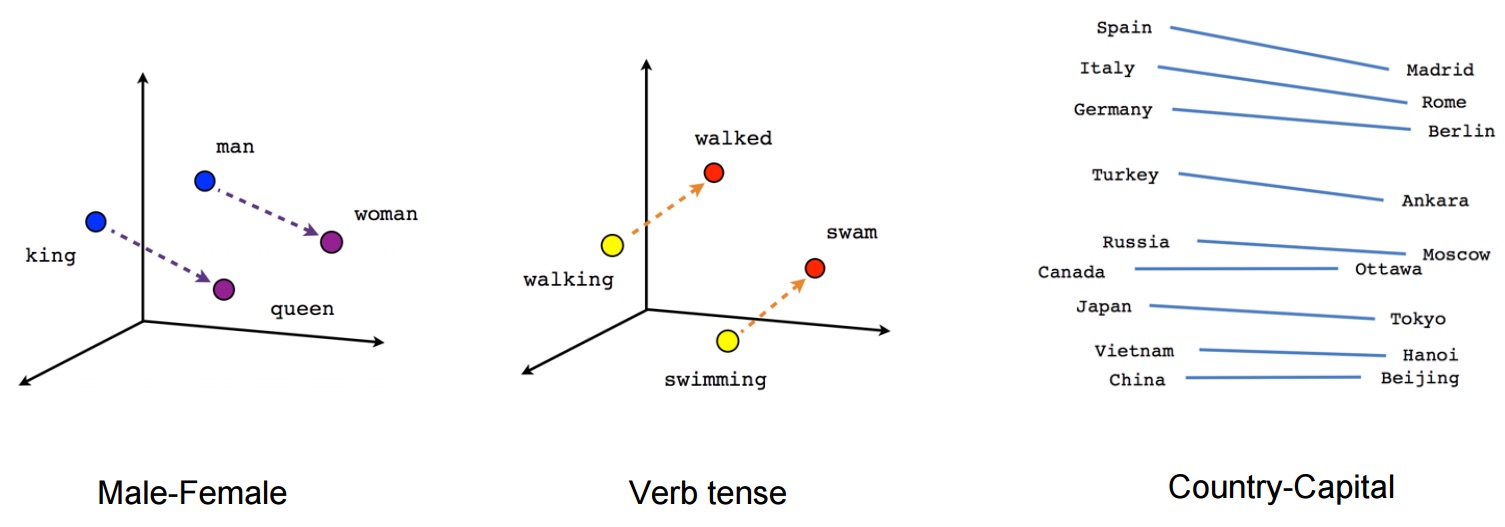In natural language processing, words are often encoded as vectors that capture semantic relationships in ad hoc, linear ways. Image from https://tensorflow.org/tutorials/word2vec.

For example, in natural language processing, the model word2vec learns for each word a vector representation, and what’s nice is that the model learns an ad hoc additive structure that semantically relates the vector representations of different words (a canonical example is “king $-$ man $+$ woman $\approx$ queen”); these representations are called word embeddings. Word embeddings, whether they are produced by word2vec, GloVe, or some other model, have become the de-facto encoding for words in many natural language applications.

1.4 Exercises

1. Prove that every vector space has a unique additive identity.
2. Prove that every vector space has a unique additive inverse.
3. Prove that $0v = 0$ for every $v \in V$. (Hint: Which of the six properties connects addition with scalar multiplication?)
4. What is the least number of elements that a vector space can contain? Why?

1.4 References

Linear Algebra Done Right, by Sheldon Axler.